[인공지능] Game AI 이론

Game

Multiagent Competitve environment : Contingencies(if-else)

Deterministic : 바둑, 체스처럼 Action 에 의한 state가 결정적임. Nondeterministic : 주사위게임처럼 주사위를 던진다는 행위만으로는 다음 state 가 결정적이지 않음

Turn-taking : 턴제 게임

Two-ply : 한 플레이어가 한 턴에 한 번씩만 action

Zero-sum : 누군가 이기면(+1) 누군가는 짐(-1) → 합계가 0임,          내가 비기면(0) 상대도 비김(0)

perfect-information : 게임에 필요한 모든 정보를 제공

 

게임의 가장 큰 문제는 search space 가 지나치게 크기 때문에 모든 경우의 수를 고려하여 최적을 알아내는것은 불가능하다는 것

Game tree

MAX : 나 자신

MIN : 상대 agent

S0 : Initial state

PLAYER(s) : 누구 차례인지 알려주는 함수 → MIN or MAX

ACTIONS(s) : PLAYER(s) 의 action 집합

RESULT(s, a) : transition model

TERMINAL-TEST(s) : 게임이 끝난 상태라면 true, 아니면 false

UTILITY(s, p) : 게임이 끝났을 때 몇점을 줄지에 대한 함수 ( terminal state 에 대해서만 정의 )

 

MAX 는 contingent strategy 로 움직임

initial state 에서 MAX의 Action 을 정해줘야하고, 이후 MIN 이 어떤 행동을 하든 그에 맞는 MAX 의 Action이 결정되어 있어야함

 

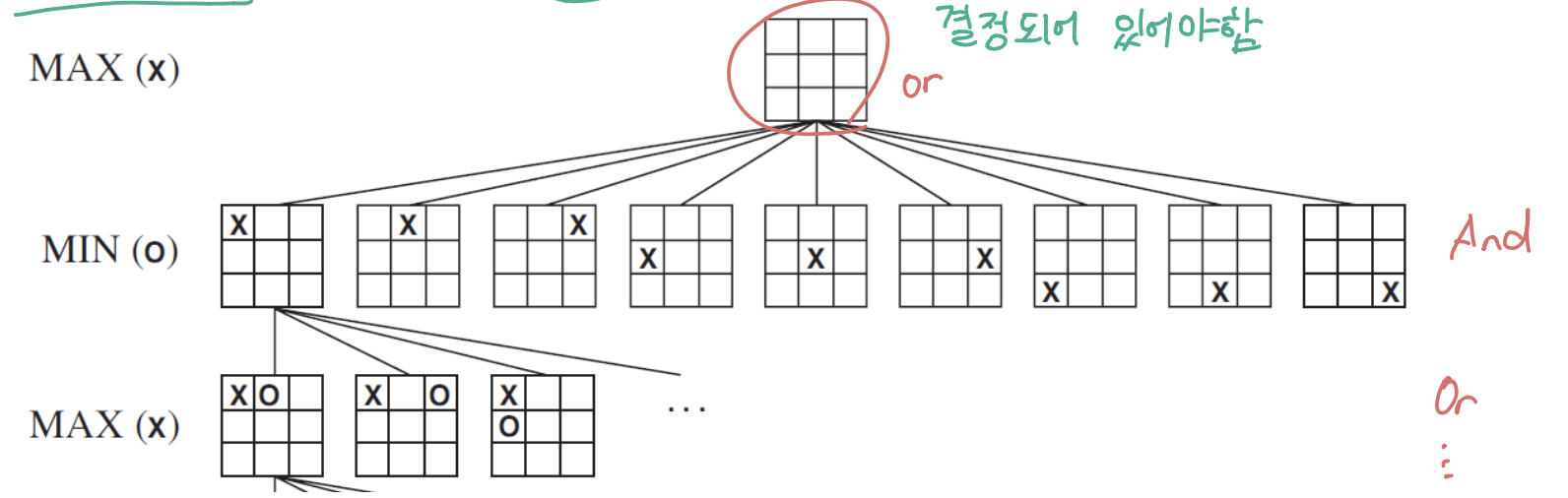
Minimax Search

MINIMAX : 노드 N에서 양 플레이어가 모두 optimal 하게 움직였을때의 utility

 

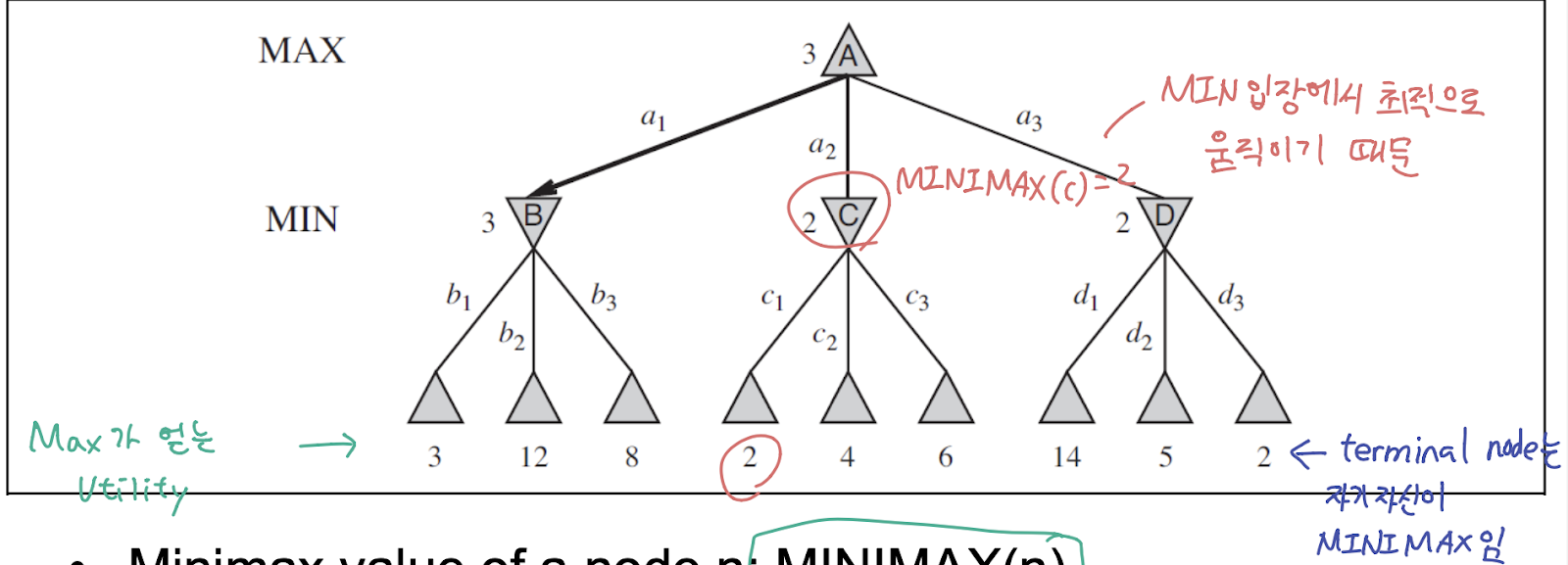
MINIMAX 가 중요한 이유는 서로 경쟁적인(Competiteve) 게임에서는 MIN 또한 자기 자신에게 최적으로 움직일 것이므로, MAX의 score 를 최소한으로 만들려고 하기 때문에 MAX는 최악의 상황을 가정하고, 거기서 최대한의 점수를 내는 방향으로 움직임

 

MINIMAX(s) =

if TERMINAL-TEST(s) → UTILITY(s)

if PLAYER(s) = MAX → maxa∈ACTIONS(s) MINIMAX(RESULT(s, a))       → MINIMAX 가 최대인 거 선택

if PLAYER(s) = MIN → mina∈ACTIONS(s) MINIMAX(RESULT(s, a))         → MINIMAX 가 최소인거 선택

 

문제점

• Search space 가 너무 큼

• 시간 복잡도만 해도 O(bm)

• b = branching factor

• m = 게임 내 수의 개수

Alpha-beta pruning

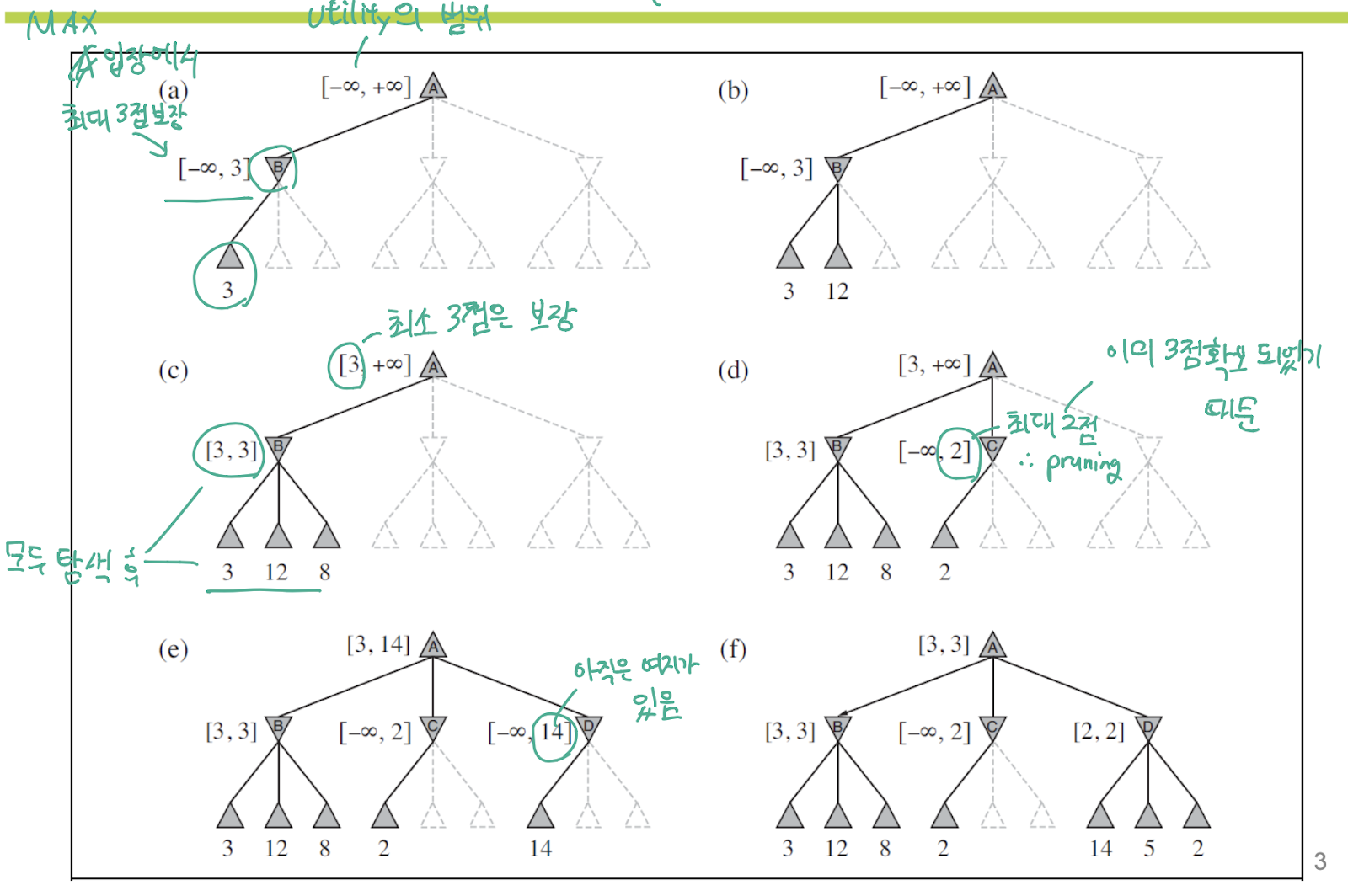
(c) : initial state A 에서 state B 로 이동했을 때 MIN 은 MAX 의 점수를 최소로 가져가는 Action 을 취할 것이므로 점수가 가장 낮은 것(3점)을 MINMAX 값으로 선정한 뒤 MAX에게 통보.  나에게로 오면 최악의 경우 3점을 줄 수 있어!

(d) : pruning 되는 대표적인 케이스로, 첫 번째 자식이 2임. 이것은 기존에 얻었던 3점보다 낮은 점수로 MAX 입장에서는 해당 state 로 갈 이유가 없음

(f) : d 와 마찬가지로 MINIMAX 가 2이므로 갈 이유가 없음

 

Alpha : MAX’s best choice = 최대 점수

Beta : MIN’s best choice = 최소 점수

 

탐색 순서에 따라 pruning 의 정도가 다르므로 이를 개선하기 위함

최적의 순서로 간다면 sqrt(b)m 까지 가능

하지만 이것은 불가능하니 랜덤으로 한다면 b3/4m 까지는 가능함

Heuristic minimax

시간과의 타협으로 인해 완벽하지 않은 alpha-beta search

H-MINIMAX(s, d) = 

if CUTOFF-TEST(s, d) → EVAL(s)

if PLAYER(s) = MAX → maxa∈ACTIONS(s) H-MINIMAX(RESULT(s, a), d + 1)

if PLAYER(s) = MAX → mina∈ACTIONS(s) H-MINIMAX(RESULT(s, a), d + 1)

 

CUTOFF-TEST = terminal node 가 너무 깊은 곳에 있어서 적당한 depth 에서 cutoff 하는 것

EVAL(s) = UTILITY 함수 대신 온 것

H-MINIMAX 에 d + 1 은 현재 상태의 depth 값을 추적하기 위함

Evaluation function

기대되는 utility 의 추정 값

좋은 evalutation function

• eval() 로 terminal state 를 평가했을 때 utility 함수와 동일한 값을 가져야함

• 즉 UTILITY(A) > UTILITY(B) 이면 EVAL(A) > EVAL(B) 여야함

• Computation 시간이 적게 걸려야함

• Nonterminal state 와는 이길 확률로 연관되어야 함

• 위 세 조건을 모두 보장할 필요는 없으며 한 두개 정도는 괜찮음

Evaluation function In Chess 

말의 수로 평가함. 좋은 말 일수록 가중치를 두는 방식(Weighted linear function) 을 사용하기도 함

EVAL(s) = w1 * f1(s) + w2 * f2(s) + … + wn * fn(s)

 

Endgame database : 게임 후반부에 다다르면 경우의 수가 적으므로 이 때의 최선의 패턴을 미리 학습해두는 것

Monte carlo tree search : 알파고가 사용한 방법으로 트리 전체가 아닌 확률이 높은 일부분만 탐색하는 방법