사과와 바나나 (boj 3114)

오늘은 사과와 바나나 문제를 풀어봤어요

R * C 크기의 땅에 두 국가 A, B가 있어요. A나라는 Apple(사과)를 좋아하고, B 나라는 Banana(바나나)를 좋아해요.

각 땅은 1 * 1 격자로 쪼개어져 있고, 격자 한 칸에는 사과나무 혹은 바나나 나무가 심어져 있고, 각 생산량은 입력으로 주어져요.

A 국가와 B국가는 불도저로 땅을 밀어버려서 국경선을 그으려고 해요. 국경선의 아래쪽은 A 국가, 윗 쪽은 B 국가의 땅이고, 불도저가 지나간 자리는 나무가 모두 사라져요. 불도저는 맨 왼쪽 위에서 출발하여 맨 오른쪽 아래에 도착할 때까지 이동하며, 한 번 이동할 때 한 칸 아래, 한 칸 오른쪽, 한 칸 오른쪽 아래 대각선으로 이동할 수 있어요.

이때 어떻게 하면 A 국가의 사과 생산량과 B국가의 바나나 생산량의 합이 최대가 되게 국경선을 그을 수 있는지 결정하는 문제예요

 

입력

첫째 줄에 땅의 크기 R과 C가 주어진다. (2 ≤ R, C ≤ 1500)

다음 R개 줄에는 각 칸에 심어져 있는 나무와 개수가 주어진다. 사과는 A, 바나나는 B이고, 각 칸에 심어져 있는 나무의 개수는 1보다 크거나 같고, 99보다 작거나 같다.

 

출력

가능한 합 중 가장 큰 것을 출력한다. 

 

예제 입력

4 3
B2 B3 B5
A3 B1 A1
A2 A4 B1
B1 B3 A3

예제 출력

17

이 문제는 dp로 풀 수 있어요. 다만 구간합 구하기 알고리즘을 알아야 하니 참고 부탁드려요 (너무 쉬워요.. 5분 컷 가능...)

 

예제 입력

 

노란색은 바나나, 빨간색은 사과 생산량이에요

 

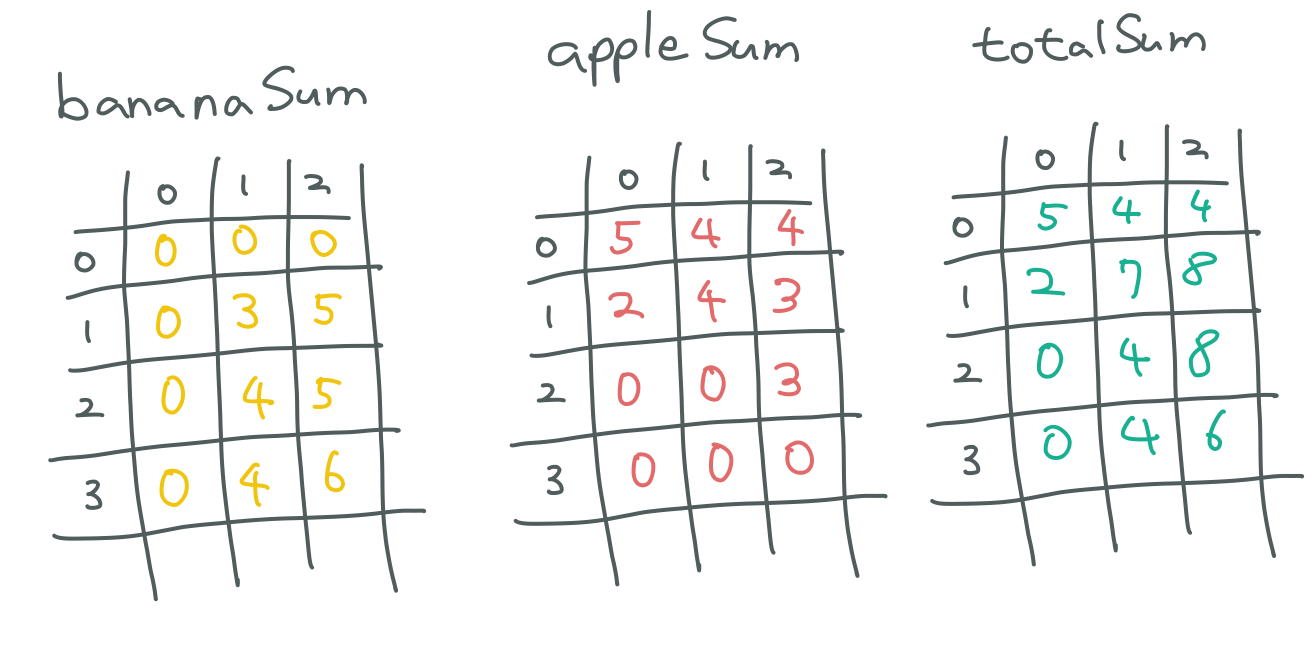
각각의 생산량을 구한 테이블이에요

보실 때 열 단위로 보시는 게 좋아요. 전체적으로 보면 전혀 이해가 안 되니까요

 

기본적으로 위 테이블의 정의는 다음과 같아요

bananaSum[n][m] = 불도저가 (n, m)에 있을 때 B국가의 바나나 생산량

appleSum[n][m] = 불도저가 (n, m)에 있을 때 A 국가의 사과 생산량

totalSum[n][m] = 불도저가 (n, m)에 있을 때 B국가의 바나나 생산량 + A국가의 사과 생산량

(bananaSum, appleSum 은 totalSum을 구할 때 생각하기 편해서 그냥 그린 거예요)

 

하지만 bananaSum의 0열을 보면 다 0인 게 좀 이상하죠? 초기화할 때의 예외처리인데

0열의 경우 0행에서부터 불도저가 다 밀면서 오는 경우밖에 없어서 2행 0열에 왔다는 건 0행 0열, 1행 0열을 무조건 지나쳐올 수밖에 없으므로 바나나 나무는 다 사라져 있을 거예요 그래서 0열의 경우에는 무조건 0으로 초기화해뒀어요 (실제로 그렇게 하지 않으면 결과가 다르게 나와요)

 

 

dp 또한 0열은 totalSum의 0열을 그대로 가져오고요.

1열부터 dp 점화식을 돌려야 해요

 

점화식은 다음과 같아요

dp[n][m] = max(

    dp[n - 1][m - 1] + totalSum[n][m],    // 왼쪽 위에서 불도저가 대각선으로 내려온 경우

    dp[n][m - 1] + totalSum[n][m],         // 왼쪽에서 불도저가 오른쪽으로 이동한 경우

    dp[n - 1][m] - apple[n][m]                // 위에서 불도저가 내려온 경우 apple[n][m] = 땅 (n, m)의 사과 생산량 (appleSum 아님)

)

 

dp[n - 1][m] - apple [n][m]에서 주의할 점은 한 땅에서 사과 혹은 바나나 둘 중 하나만 생산되기에, 해당 땅이 바나나를 생산하는 땅이라면 0을 빼야 한다는 거예요

 

dp[1][1] 을 구해볼게요

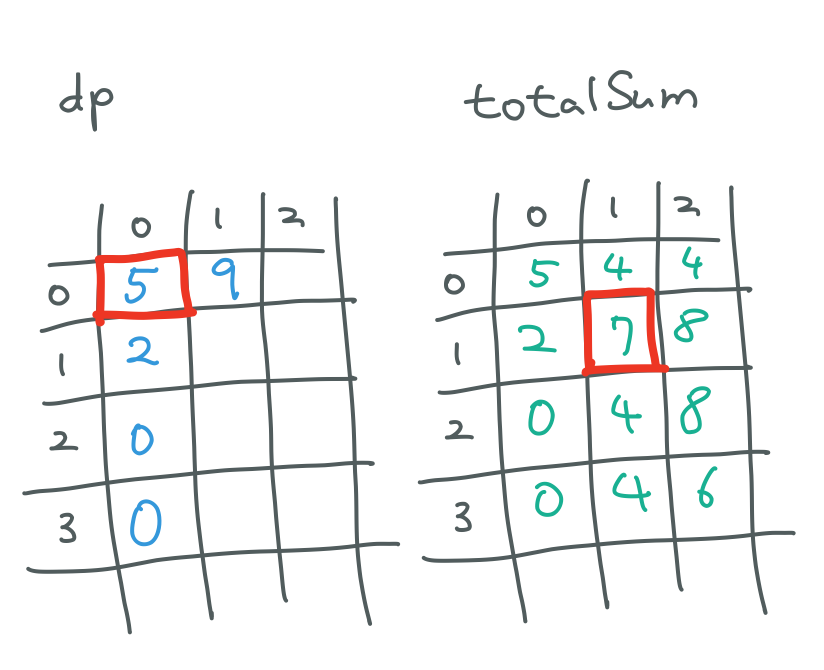
5 + 7 = 12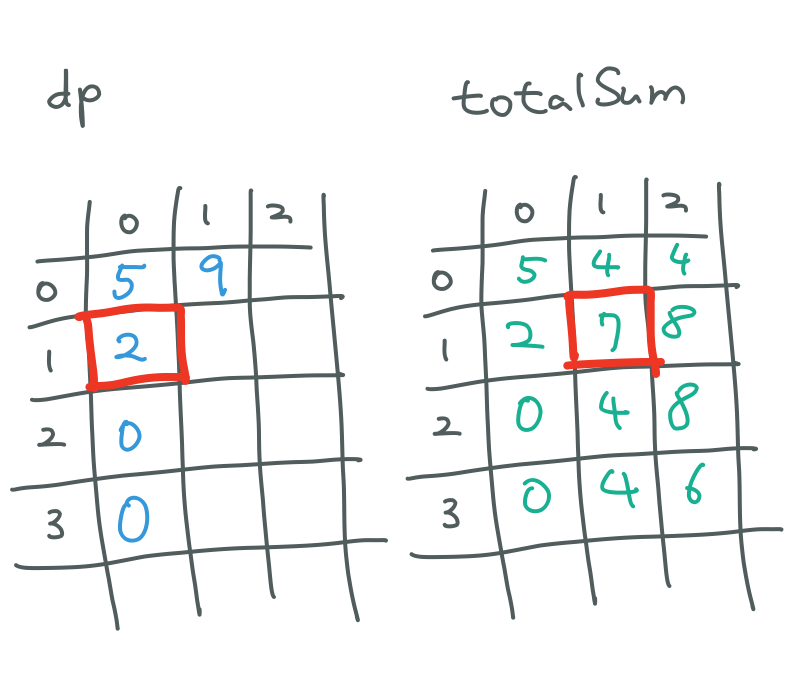

 

2 + 7 = 9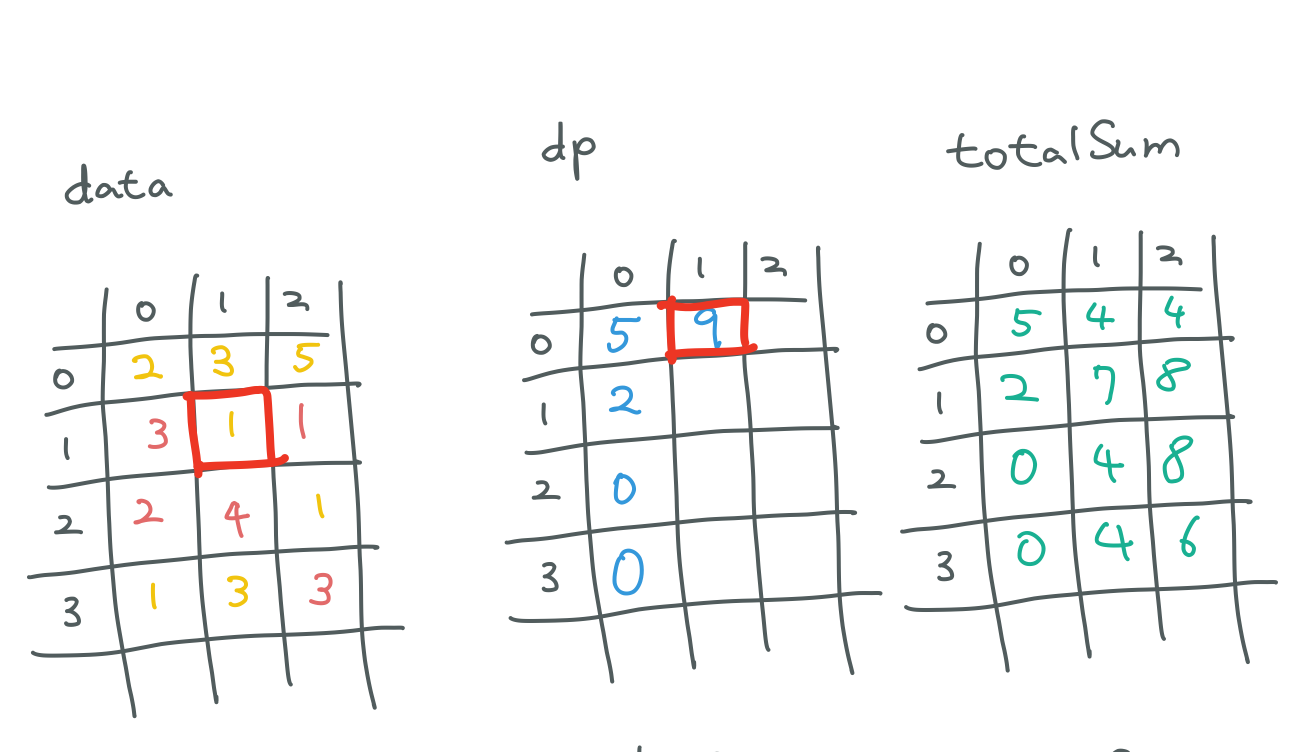

 

9 - 0 = 9

가장 큰 값은 왼쪽 위에서 오는 12네요

따라서 dp[1][1] = 12

 

 

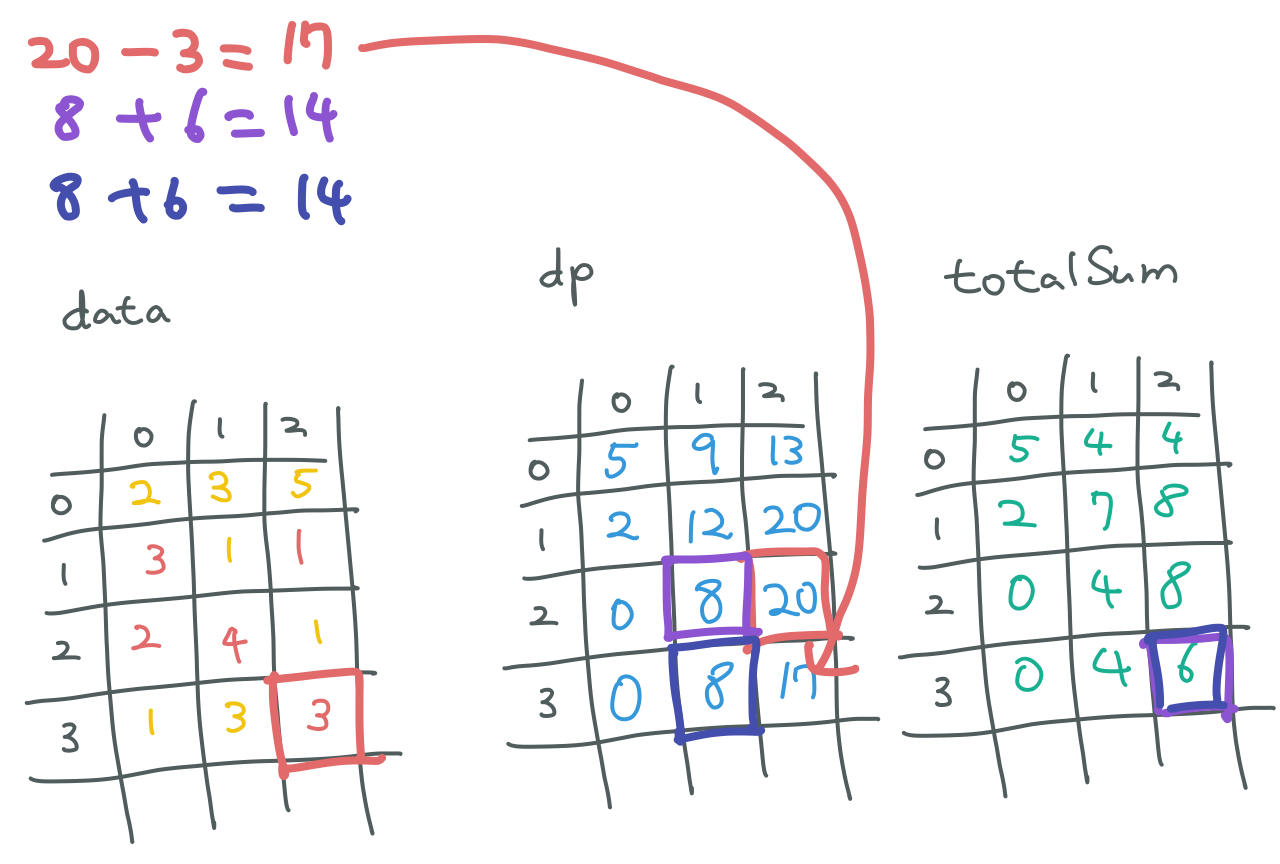
위에서 내려오는 경우가 위 사진과 같아요 dp[3][2] 를 구할 때 보시면 20에서 3을 빼어 17이 된 값이 가장 큼을 볼 수 있어요

 

 

소스코드 

#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <memory.h>

#define NW 0
#define N 1
#define W 2

int R, C;
std::pair<char, int> map[1510][1510];
std::pair<char, int> p;
int appleSum[1510][1510];
int bananaSum[1510][1510];
int totalSum[1510][1510];
int dp[1510][1510];
//int path[1510][1510];

//void printPath(int y, int x) {
//    if (y == 0 && x == 0)
//        return;
//
//    if (path[y][x] == NW)
//        printPath(y - 1, x - 1);
//    else if (path[y][x] == N)
//        printPath(y - 1, x);
//    else
//        printPath(y, x - 1);
//
//    printf("%d %d\n", y, x);
//}


int main(void) {
//    freopen("input.txt", "r", stdin);
    scanf("%d %d", &R, &C);
    int apple, banana;

    for (int r = 1; r <= R; r++) {
        for (int c = 1; c <= C; c++) {
            getchar();
            scanf("%c%d", &p.first, &p.second);
            map[r][c] = p;
        }
    }

    for (int c = 2; c <= C; c++) {
        for (int r = 1; r <= R; r++) {
            banana = map[r - 1][c].first == 'B' ? map[r - 1][c].second : 0;
            bananaSum[r][c] = bananaSum[r - 1][c] + banana;
        }
    }

    for (int r = R; r > 0; r--) {
        for (int c = C; c > 0; c--) {
            apple = map[r + 1][c].first == 'A' ? map[r + 1][c].second : 0;
            appleSum[r][c] = appleSum[r + 1][c] + apple;
        }
    }

    for (int r = R; r > 0; r--) {
        for (int c = C; c > 0; c--) {
            totalSum[r][c] = bananaSum[r][c] + appleSum[r][c];
        }
    }

    for (int r = 1; r <= R; r++) {
        dp[r][1] = totalSum[r][1];
    }

    for (int c = 2; c <= C; c++) {
        for (int r = 1; r <= R; r++) {
            apple = map[r][c].first == 'A' ? map[r][c].second : 0;
            dp[r][c] = std::max(
                    std::max(dp[r - 1][c - 1], dp[r][c - 1]) + totalSum[r][c],
                    dp[r - 1][c] - apple
            );

//            if (dp[r][c] == dp[r - 1][c - 1] + bananaSum[r - 1][c] + appleSum[r + 1][c]) {
//                path[r][c] = NW;
//            } else if (dp[r][c] == dp[r][c - 1] + bananaSum[r - 1][c] + appleSum[r + 1][c]) {
//                path[r][c] = W;
//            } else {
//                path[r][c] = N;
//            }
        }
    }

//    printPath(R, C);
    printf("%d", dp[R][C]);
    return 0;
}