DFS 메모이제이션

오늘은 DFS 메모이제이션 기법에 대해 알아볼거에요

이 기법은 DFS 문제를 조금 더 최적화 시킨 기법으로, 개념 자체는 매우 간단해요

"한 번 갔던 곳의 DFS 결과 값을 저장해두고 나중에 이 곳에 다시 방문하면 또 탐색하지 말고 이 값을 재사용하자!" 라는 생각인거죠

메모이제이션 기법은 N이 커질수록 그 빛을 발하니 꼭 익혀두는게 좋아요

N * N 짜리 2차원 배열이 있다고 하고, 우리는 값이 점점 커지는 최대 경로를 구하는 문제가 있다고 합시다.

아래와 같은 배열의 경우에는

1	2	3
5	6	4
7	6	5

1	2	3
5	6	4
7	6	5

분홍색으로 칠해진 부분이 정답이 될거에요

 

일반적인 DFS로도 충분히 구할 수 있지만 그렇게 되면 계산의 중복이 심해져서 매우 느린 알고리즘이 될 수 있어요

여기서 예를 들면 table[0][2] 는 정답인 경우에도 한 번 구해지고,

table[0][0] -> table[1][0] -> table[2][0] 로 가는 경로에서도 구해지게 돼요

 

지금은 N 이 작아서 겨우 하나 겹치는것처럼 보이지만 table[0][2] 에서 갈 수 있는 경로의 길이가 100이 넘었다면?

길이가 100이 넘는 경로를 두번,세번, 네번 중복해서 구하게되니 매우 비효율적이겠죠?

 

그래서 우리는 lookup 테이블을 만들어서 이 값들을 저장해둘거에요

lookup[i][j] = ( i , j ) 에서 시작하는 가장 긴 경로의 길이

이렇게 저장해두고 구해보죠

 

아래와 같은 입력이 주어졌다고 할 때

1	10	11	4
2	3	4	5
7	6	5	6
9	8	6	7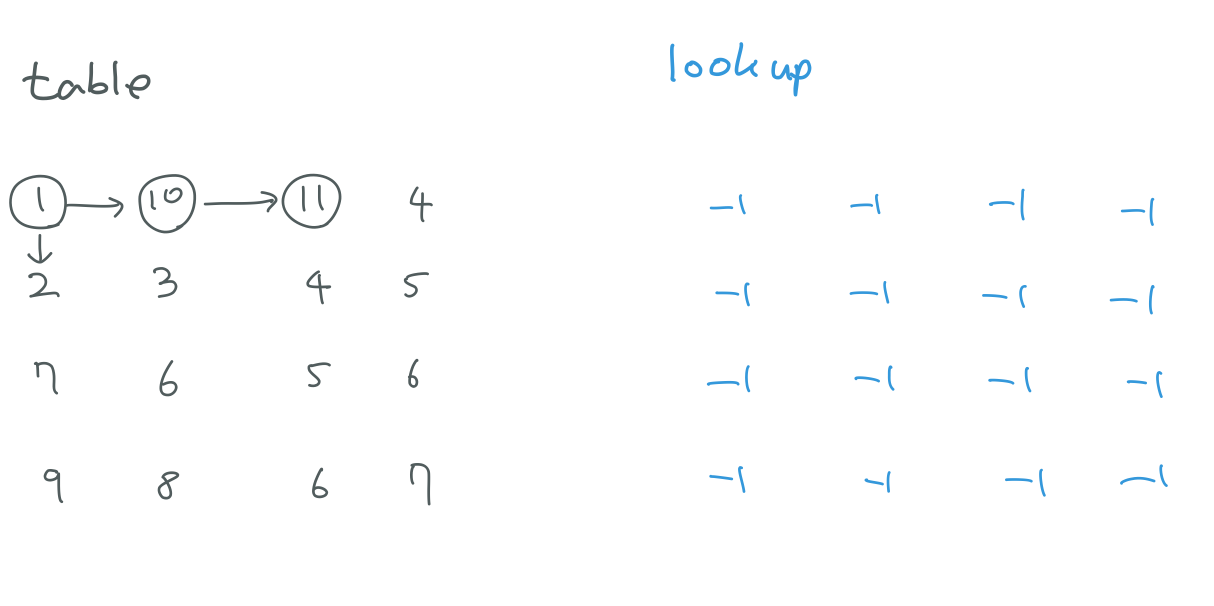

 

lookup 이 다 비워 있을때는 평범하게 DFS 를 돌려요. 대신 아래 사진을 보면 lookup[0][1], lookup[0][2] 가 값이 바뀐것을 확인할 수 있어요. 빨강색으로 표현된건 값이 확정된 곳들을 의미해요. 따라서 빨강색 글씨로 된 곳을 다시 방문하게 됐을 때는 DFS 를 새로 돌려서 값을 다시 구하는게 아니라 lookup 값을 바로 리턴해버리면 중복 연산을 피할 수 있게 되는거에요

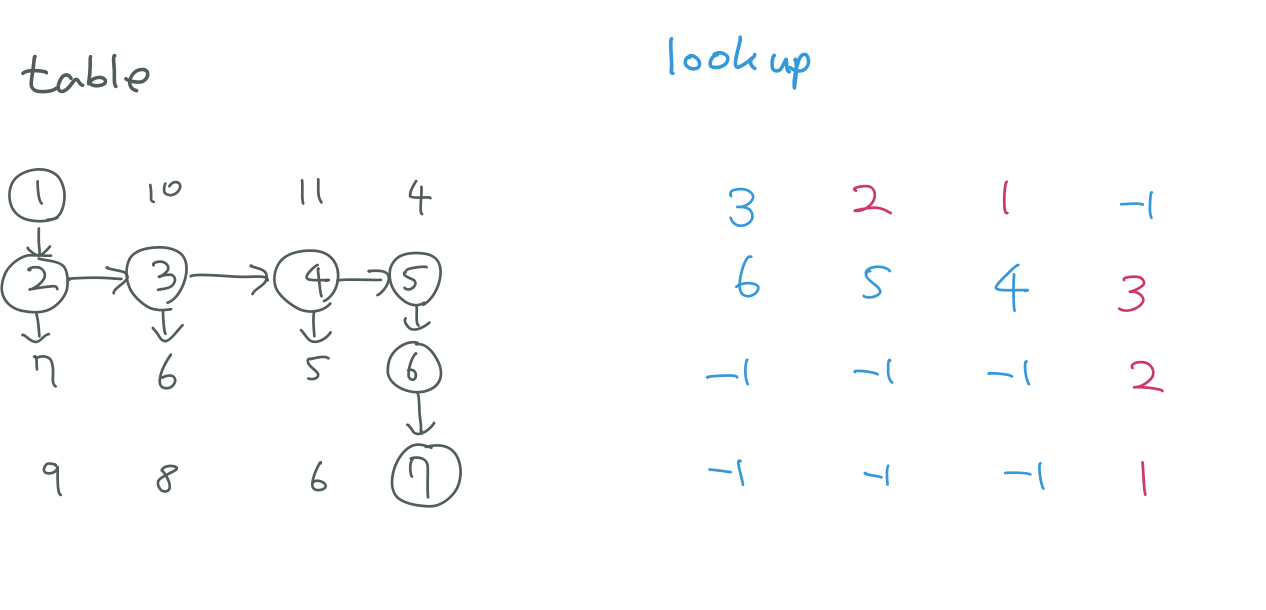
위 사진도 마찬가지로 5, 6, 7부분이 lookup 상에서 3, 2, 1 로 확정된 것을 확인할 수 있어요

DFS(2, 2) 를 구하는 과정에서 lookup[2][3] 값을 바로 가져오는 것을 볼 수있어요. 메모이제이션을 쓰지 않았다면 DFS(2, 3) 을 돌려서 그 경로의 길이를 다시 구했을 거에요. 같은 규칙을 적용해서 모든 경로의 길이를 구하는 모습을 확인할 수 있어요

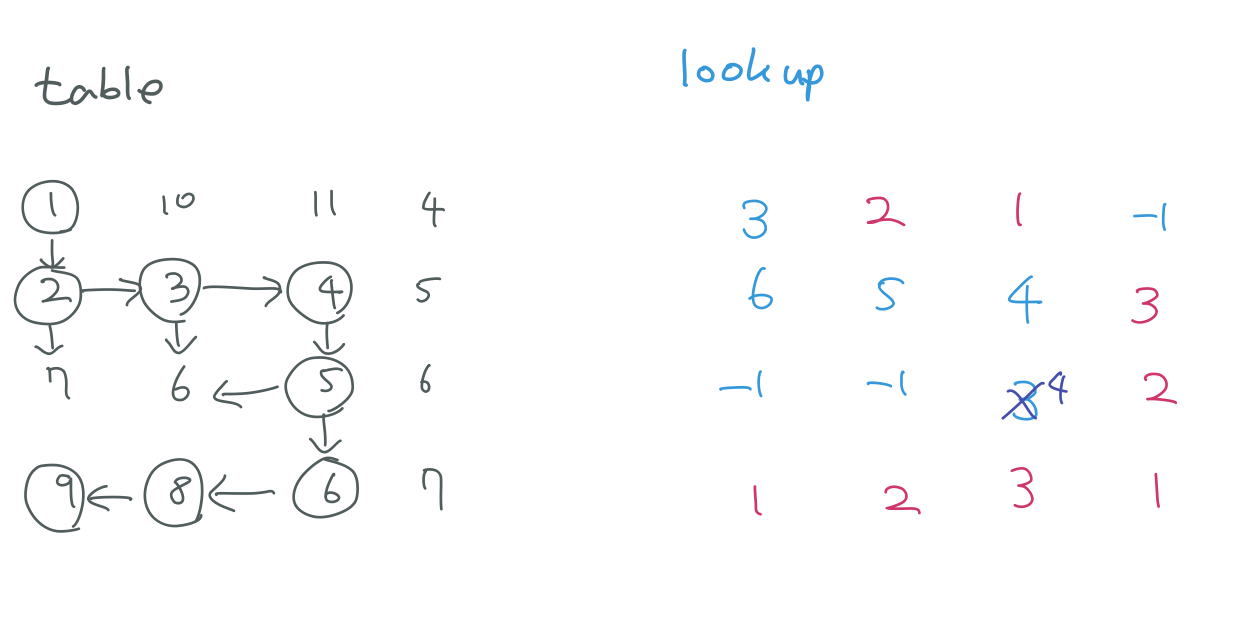
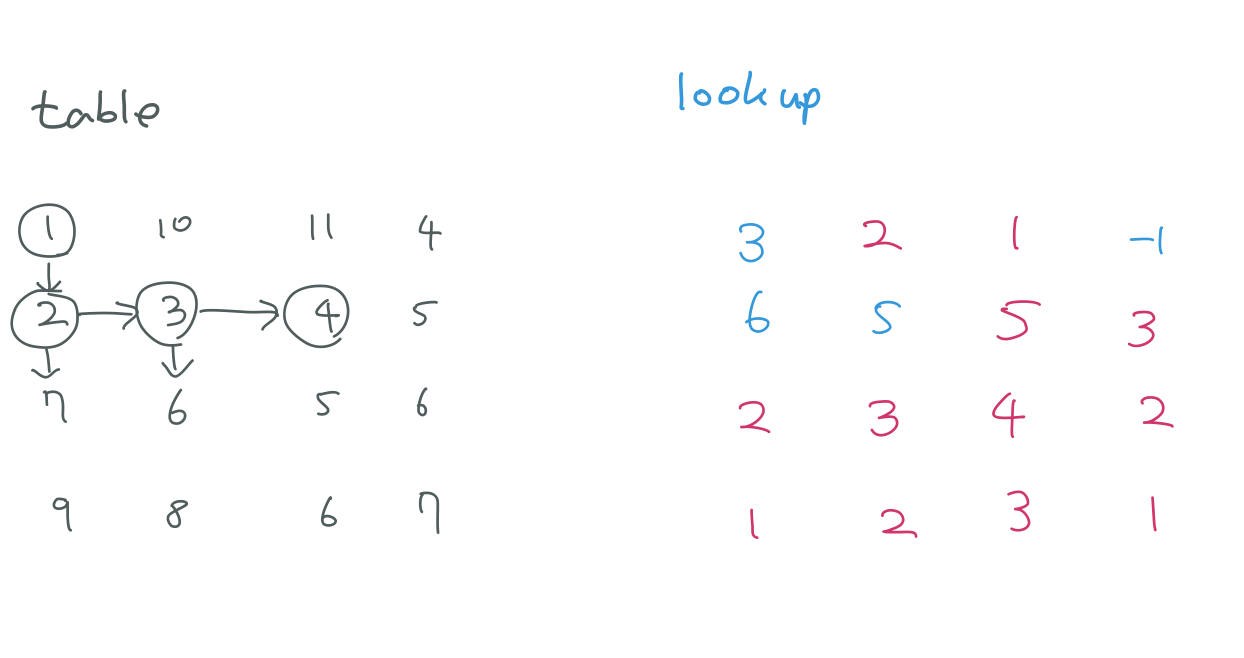
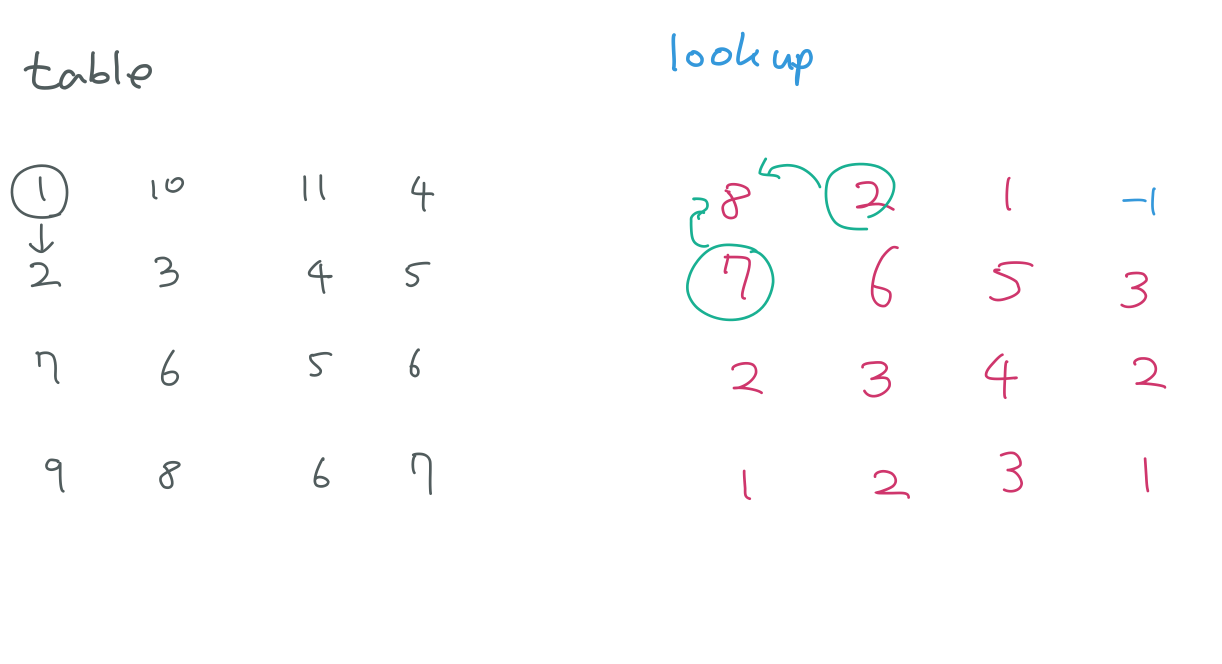
DFS(0, 0) 의 경우에도 원래라면 DFS(1, 0)과 DFS(0, 1) 을 돌려야하는데 메모이제이션 기법으로 인해 lookup[1][0], lookup[0][1] 을 그대로 끌어오는 모습을 볼 수 있어요

 

예제 문제로 욕심쟁이 팬더 문제가 있어요! 직접 풀어보시면 도움이 될 것 같네요

 

소스코드는 다음과 같습니다.

#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <memory.h>

int N;
int map[510][510];
int lookup[510][510];
int direction[4][2] = {
        {-1, 0},
        {0, 1},
        {1, 0},
        {0, -1}
};
int globalMax;

int solution(int y, int x) {
    if (lookup[y][x] != -1)
        return lookup[y][x];

    int max = 0;
    for (int i = 0; i < 4; i++) {
        int newY = y + direction[i][0];
        int newX = x + direction[i][1];

        if (newY < 0 || newY >= N || newX < 0 || newX >= N || map[y][x] >= map[newY][newX])
            continue;

        max = std::max(max, solution(newY, newX));
    }

    lookup[y][x] = max + 1;
    globalMax = std::max(globalMax, lookup[y][x]);
    return lookup[y][x];
}

int main(void) {
    scanf("%d", &N);
    for (int y = 0; y < N; y++) {
        for (int x = 0; x < N; x++) {
            scanf("%d", map[y] + x);
        }
    }

    memset(lookup, -1, sizeof(lookup));
    for (int y = 0; y < N; y++) {
        for (int x = 0; x < N; x++) {
            solution(y, x);
        }
    }

    printf("%d", globalMax);
    return 0;
}