MT 문제 (boj 10265)

오늘은 MT 문제에 대해 풀어볼게요

저는 문제를 딱 보는 순간 위상정렬(Topological sort) 문제라는게 보였어요

 

위 입력은 다 자기 자신을 지목한 상황이라 다른 사람에게 의존하지 않는 경우에요

 

세 번째 그림을 잘 보셔야해요

1은 2가 가야 가는 것이지만 2가 간다고 무조건 1이 가야하는건 아니에요. 따라서 세 번째 입력의 경우에도 답은 2명이 됩니다.

 

사실 여기까지는 단순한 위상정렬 문제로 보여요. 의존성이 없는 사람부터 버스에 태우면서 k명이 될때까지 최대한 태워보면 되니까요

 

하지만 예외가 있습니다.

이런 경우는 조금 다르죠 1, 2, 3 은 서로 의존적이라 다 같이 가거나 다 같이 안 갈 수 밖에 없어요.

따라서 답은 1명이 됩니다.

 

그냥 위상 정렬로 풀려고 해도 쉽지 않아요.

왜냐면 1, 2, 3은 서로 의존적이라 선행 과제의 수가 모두 1이라서 선행과제가 0인 과제들을 처리하는 위상정렬 기법으로는 어렵죠

일반적인 위상정렬 기법으로 푼다면 사이클을 의미하는 Back edge를 임의적으로 끊어내는 방식으로 풀겠지만

 

그렇게 풀면 세 명이 모두 의존적이라는 특성을 잃어버리게 돼요

 

따라서 저는 그래프를 SCC(Strongly Connected Component) 단위로 묶어냈어요

 

예제 입력2 원래 그래프

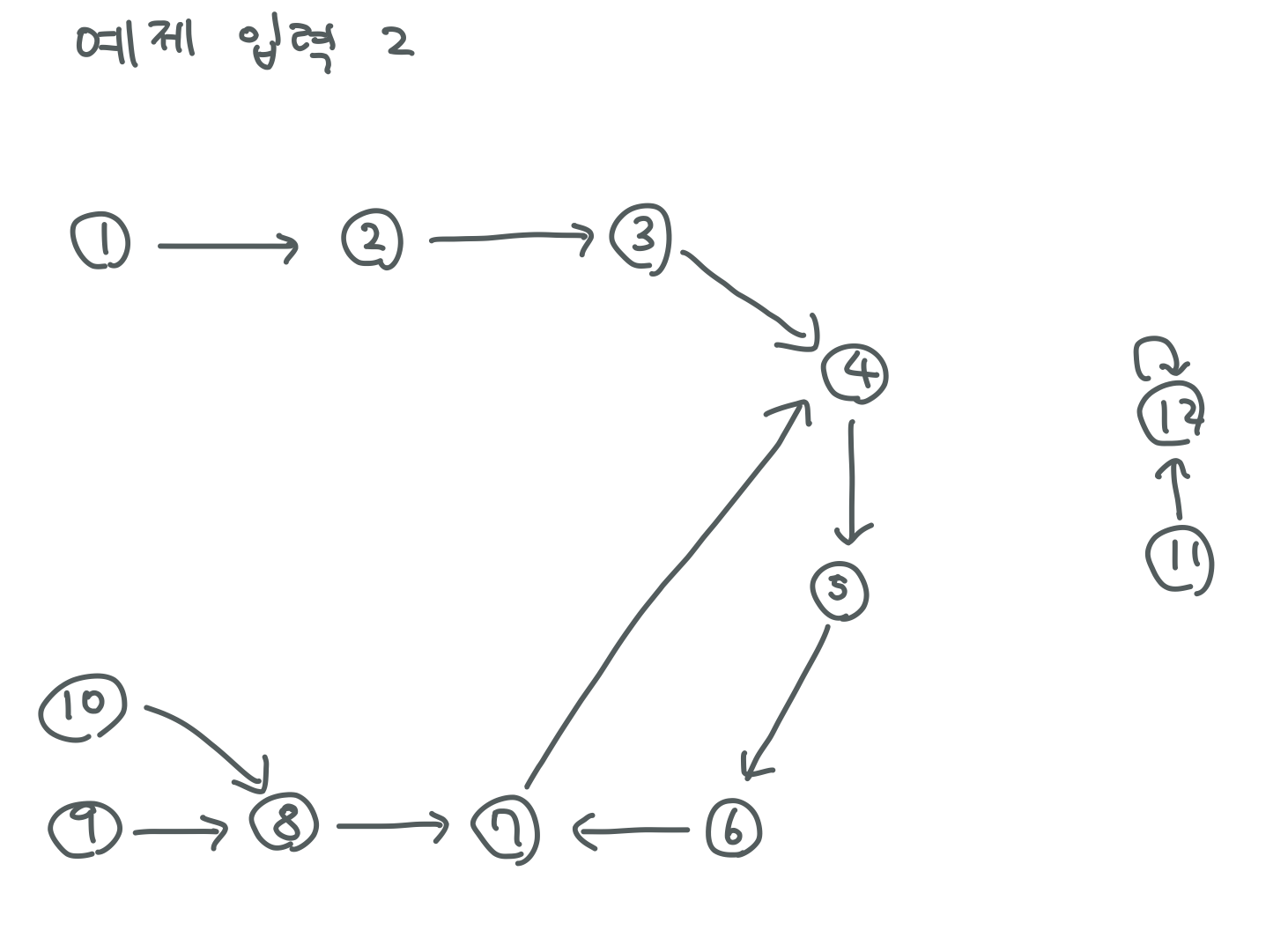
위 그래프는 선행 과제가 없는 과제가 12번 뿐입니다.

따라서 1 ~ 10번 과제는 처리하기가 어렵습니다.

 

예제 입력2 SCC 추상화

SCC로 추상화를 한 그래프는 4번 SCC가 선행과제가 없는 과제로 판별이 되었기에 1 ~ 10번 과제도 처리할 수 있습니다.

 

즉 4 5 6 7번 학생은 무조건 같이 타거나 같이 타지 않기에 하나의 세트로 묶어서 생각하는 것입니다.

이를 위해서 그래프를 학생간의 관계가 아닌 SCC 간의 관계로 바라봅니다.

 

 

이를 구하려면 위상정렬과 마찬가지로 선행 과제가 없는 SCC에서부터 DFS 를 돌립니다.

이 때 선행과제가 없는 SCC를 출발점. 즉 Root 라고 부르겠습니다.

아래 그래프에서는 4번 SCC, 12번 SCC가 각각 Root 가 될 수 있습니다.

4 ~ 10명 태울 수 있는 그룹A와 1 ~ 2명을 태울 수 있는 그룹B에서 인원을 적절히 뽑아 K명을 뽑아야하는 문제만 남았습니다.

이는 각 그룹에서 몇명을 뽑아야 K명에 최대한 가까이 태울 수 있을지 최적화 문제가 됩니다.

0-1 냅색으로 이 문제를 풀 수 있습니다.

 

인원	루트 SCC
10	4
9	4
8	4
7	4
6	4
5	4
4	4
2	12
1	12

0-1 냅색 규칙

1. 최초의 bound(한계치)는 N 입니다.

2. 현재 상태공간트리의 노드 bound 가 지금까지 구해진 max 보다 작거나 같다면 이는 유망하지 않은 노드라고 판단합니다.

3. max와 지금까지의 상태공간트리의 합계값 sum은 K를 넘어서는 안됩니다.

4. 이전 상태 공간 트리에서 처리된 root 에 대해서는 다시 처리하지 않습니다.

 

bound 계산 방법

root = 현재 노드의 루트 SCC

value = 현재 노드의 인원

f(root) = 루트 SCC가 처리할 수 있는 최대 인원    예) f(4) = 10,  f(12) = 2

 

현재 노드를 넣는 경우 : bound = bound - f(root) + value

현재 노드를 넣지 않는 경우 :

          이후 상태 공간 트리에 해당 루트 SCC가 남은 경우 : bound 그대로 유지,  아직 해당 루트 SCC가 처리될 여지가 있기 때문

          이후 상태 공간 트리에 해당 루트 SCC가 없는 경우 : bound = bound - f(root),   이제 해당 루트 SCC가 처리될 가능성이 없기 때문

주의할 점

bound 계산은 주어진 수식대로 진행하지만 상태 공간 트리에서 각 규칙에 적용할 때는 bound와 K 값 중 작은 값을 사용합니다.

그래야 max == K 가 되었을 때 2번 규칙에 의해 남은 모든 상태 공간 트리를 유망하지 않은 노드로 만들 수 있습니다.

소스코드

#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <memory.h>
#include <set>
#include <vector>
#include <stack>
#include <deque>
#include <map>
#include <queue>

#define INF 987654321

// 입력
int N, K;
int arr[1010];


int unionList[1010];

// 정방향 그래프
int graph[1010];

// 역방향 그래프
std::deque<int> invertedGraph[1010];

// SCC를 구하기 위한 스택
std::stack<int> stack;

int visited[1010];

// 선행 과제의 수
int countList[1010];

// SCC의 크기
int sccSizeList[1010];

// SCC가 처리할 수 있는 최대 인원
int maxSCCSizeList[1010];

// 총 인원
int totalSum;

// 0-1 냅색 때 사용할 아이템 (내림차순 정렬될거임)
// std::pair<인원, 루트>
std::vector<std::pair<int, int>> itemList;
std::pair<int, int> p;
int max;


/**
 * SCC를 만들기 위해 정방향 그래프에 대해 DFS
 * @param n 방문할 노드 번호
 */
void DFS(int n) {
    if (visited[n])
        return;

    visited[n] = 1;
    DFS(graph[n]);

    // 하위노드를 다 탐색한 뒤 해당 노드는 stack에 추가함
    // 이 스택에서 하나씩 빼면서 SCC로 만들어내기 때문에 윗쪽에 있는 노드일수록 먼저 SCC로 묶이게 됨
    stack.push(n);
}

/**
 * 그래프를 SCC 단위로 만드는 함수, 역방향 그래프를 DFS
 *
 * @param n 방문할 노드, stack에서 하나 씩 pop 된 순서대로 n으로 들어옴
 * @param root 루트 노드 번호
 * @param count 현재 SCC 크기
 * @return SCC 크기
 */
int makeScc(int n, int root, int count) {
    if (visited[n])
        return count - 1;

    visited[n] = 1;
    unionList[n] = root;

    if (count > 1) {
        // SCC로 묶인 노드들은 선행 과제들이 없음
        countList[n] = 0;
        countList[root] = 0;
    }

    // 역방향 그래프를 기반으로 DFS 탐색하여 하나의 SCC로 묶어냄
    for (int t : invertedGraph[n]) {
        count = makeScc(t, root, count + 1);
    }

    // SCC의 총 크기
    return count;
}

/**
 * 위상 정렬
 * SCC에서 처리할 수 있는 최대, 최소 인원을 알아내는 함수
 *
 * @param n 방문할 SCC 번호. 최초로 호출된 topologicalSort()의 n은 countList[n] == 0 인 노드만이 입력으로 들어옴 (즉 선행 과제가 없음)
 * @param size SCC가 처리한 노드의 수
 * @param root 루트 SCC 번호
 * @return SCC가 처리할 수 있는 최대 노드의 수
 */
int topologicalSort(int n, int size, int root) {
    if (visited[n])
        return size;

    visited[n] = 1;
    size += sccSizeList[n];
    if (sccSizeList[n] > 0) {
        p = {size, root};
        itemList.push_back(p);
    }

    // 역방향 그래프로의 DFS는 본인이 버스에 탐으로서 버스를 탈 수 있게된 학생들을 모두 탐색함
    for (int t : invertedGraph[n]) {
        size = topologicalSort(t, size, root);
    }
    return size;
}

/**
 * 0-1 냅색을 하는 함수
 *
 * @param n n 번째 아이템으로, itemList[n]을 의미
 * @param sum 현재 상태공간트리 노드까지의 결과값의 합
 * @param bound 현재 상태공간트리 노드에서 최대로 다다를 수 있는 이상적인 한계치 bound
 */
void search(int n, int sum, int bound) {
    // 현재까지 구한 max 값보다 bound가 작거나 같으면 유망하지 않음
    // 모든 itemList를 방문한 경우 끝
    if (std::min(bound, K) <= max || n == itemList.size())
        return;

    // 이미 방문한 root는 다시 방문하지 않음
    if (visited[itemList[n].second]) {
        search(n + 1, sum, bound);
        return;
    }

    // sum과 현재 노드의 value를 더한 값이 K보다 크면 해당 노드는 건너뜀
    // 유망하지 않은것이 아님.
    // 내림차순 정렬이기에 이후에 K보다 작거나 같은 노드가 등장할 여지가 충분함
    if (sum + itemList[n].first > K) {
        visited[itemList[n].second] = 0;

        // 이제 더는 상태공간트리에 root SCC의 노드가 등장하지 않을 것이기에 root가 처리하는 인원들은 bound 계산에서 완전히 제외
        if (itemList[n].first == sccSizeList[itemList[n].second]) {
            search(n + 1, sum, bound - itemList[n].first);
        }

        // 아직 상태공간 트리에 root SCC의 노드가 등장할 수 있기에 아직은 bound 계산에 포함
        else {
            search(n + 1, sum, bound);
        }
        return;
    }

    // 현재까지 sum과 value 의 합이 지금까지 구한 max보다 크다면 max를 교체
    max = std::max(max, sum + itemList[n].first);

    visited[itemList[n].second] = 1;
    search(n + 1, sum + itemList[n].first, bound - maxSCCSizeList[itemList[n].second] + itemList[n].first);

    visited[itemList[n].second] = 0;

    // 이제 더는 상태공간트리에 root SCC의 노드가 등장하지 않을 것이기에 root가 처리하는 인원들은 bound 계산에서 완전히 제외
    if (itemList[n].first == sccSizeList[itemList[n].second]) {
        search(n + 1, sum, bound - itemList[n].first);
    }

        // 아직 상태공간 트리에 root SCC의 노드가 등장할 수 있기에 아직은 bound 계산에 포함
    else {
        search(n + 1, sum, bound);
    }
}

int main() {
    scanf("%d %d", &N, &K);
    for (int n = 1; n <= N; n++) {
        scanf("%d", arr + n);
        graph[n] = arr[n];
        invertedGraph[arr[n]].push_back(n);

        if (n != arr[n])
            countList[n] = 1;
    }

    // SCC 구하기위한 DFS
    for (int n = 1; n <= N; n++) {
        DFS(n);
    }

    // 본격적인 SCC 구하기
    memset(visited, 0, sizeof(visited));
    while (!stack.empty()) {
        int t = stack.top();
        stack.pop();
        sccSizeList[t] = makeScc(t, t, 1);
    }

    // 각 SCC에서 처리할 수 있는 최대, 최소 인원을 구함
    memset(visited, 0, sizeof(visited));
    for (int n = 1; n <= N; n++) {
        if (countList[n] == 0) {
            maxSCCSizeList[n] = topologicalSort(n, 0, n);
            totalSum += maxSCCSizeList[n];
        }
    }

    // SCC에서 처리할 수 있는 인원들을 내림차순으로 정렬
    std::sort(itemList.begin(), itemList.end(), std::greater<std::pair<int, int>>());

    memset(visited, 0, sizeof(visited));

    // 0-1 Knapsack
    search(0, 0, totalSum);

    // 최대 인원 출력
    printf("%d", max);
    return 0;
}