-
AI Linear regression 파이썬 구현인공지능 2020. 5. 24. 16:51728x90
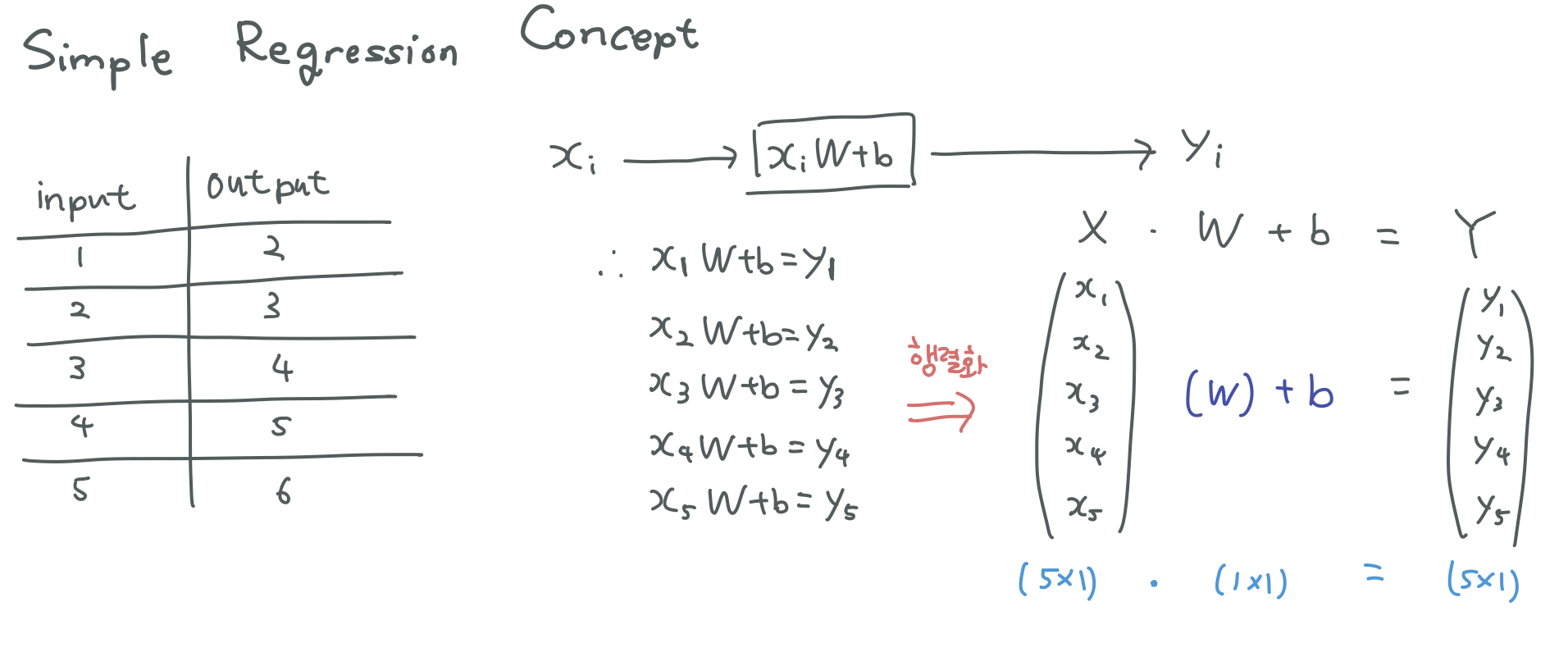
지금까지 y = Wx + b 라고 표현했지만 행렬 dot product를 통해 계산을 해내려면 y = xW + b 라고 생각하는게 좋습니다.
그렇게 되면 입력 값(x)의 집합 X 와 X * W + b 로 나온 결과의 집합(Y) 를 구할 수 있고, 실제 정답의 집합 T와의 오차가 최소인 W, b 를 구하는것이 목표입니다.
Training data 준비
# 입력 데이터와 출력 데이터 셋을 (5 * 1) 행렬로 변환(reshape) x_data = np.array([1, 2, 3, 4, 5]).reshape(5, 1) y_data = np.array([2, 3, 4, 5, 6]).reshape(5, 1)임의의 W, b 준비
# 최초로 등록될 임의의 W, b 설정 # 0 ~ 1사이의 값으로 (1 * 1)짜리 matrix 생성 W = np.random.rand(1, 1) # 0 ~ 1 사이의 numpy scalar b = np.random.rand(1)Loss Function 준비
def loss_func(x, t): # Y = X * W + b y = np.dot(x, W) + b # 각 오차들의 제곱의 합 평균 return np.sum((t - y) ** 2) / len(x)미분 함수 준비
# 미분 함수 def numerical_derivative(fx, input_list): delta_x = 1e-4 ret = np.zeros_like(input_list) it = np.nditer(input_list, flags=['multi_index'], op_flags=['readwrite']) while not it.finished: i = it.multi_index tmp = input_list[i] input_list[i] = float(tmp) - delta_x f1 = fx(input_list) input_list[i] = float(tmp) + delta_x f2 = fx(input_list) ret[i] = (f2 - f1) / (delta_x * 2) input_list[i] = tmp it.iternext() return ret # 오차를 알려주는 함수 def error_val(x, t): y = np.dot(x, W) + b return np.sum((t - y) ** 2) / len(x) # 학습 이후에 예측해주는 함수 def predict(x): y = np.dot(x, W) + b return y학습
# 학습 가중치 learning_rate = 1e-2 f = lambda x: loss_func(x_data, y_data) print("Initial error value = ", error_val(x_data, y_data), "initial W = ", W, "initial b = ", b) for step in range(8001): # 학습 W -= learning_rate * numerical_derivative(f, W) b -= learning_rate * numerical_derivative(f, b) if step % 400 == 0: print("step = ", step, "error value = ", error_val(x_data, y_data), "W = ", W, "b = ", b)예측
# 예측 print(predict(45))결과

step 이 증가할수록 error value 가 떨어지는 모습을 보입니다.
마지막 error value 가 9.5로 증가한게 아니라 맨 뒤에 e-29로, 0.0000.. (29개)... 95로 매우 작은 수입니다.
결과가 입력값 + 1 이던 데이터에 기반해서 학습한 결과 45를 입력을 넣었을 때 46이 리턴되는 것을 알 수 있습니다.
다변수 데이터 처리
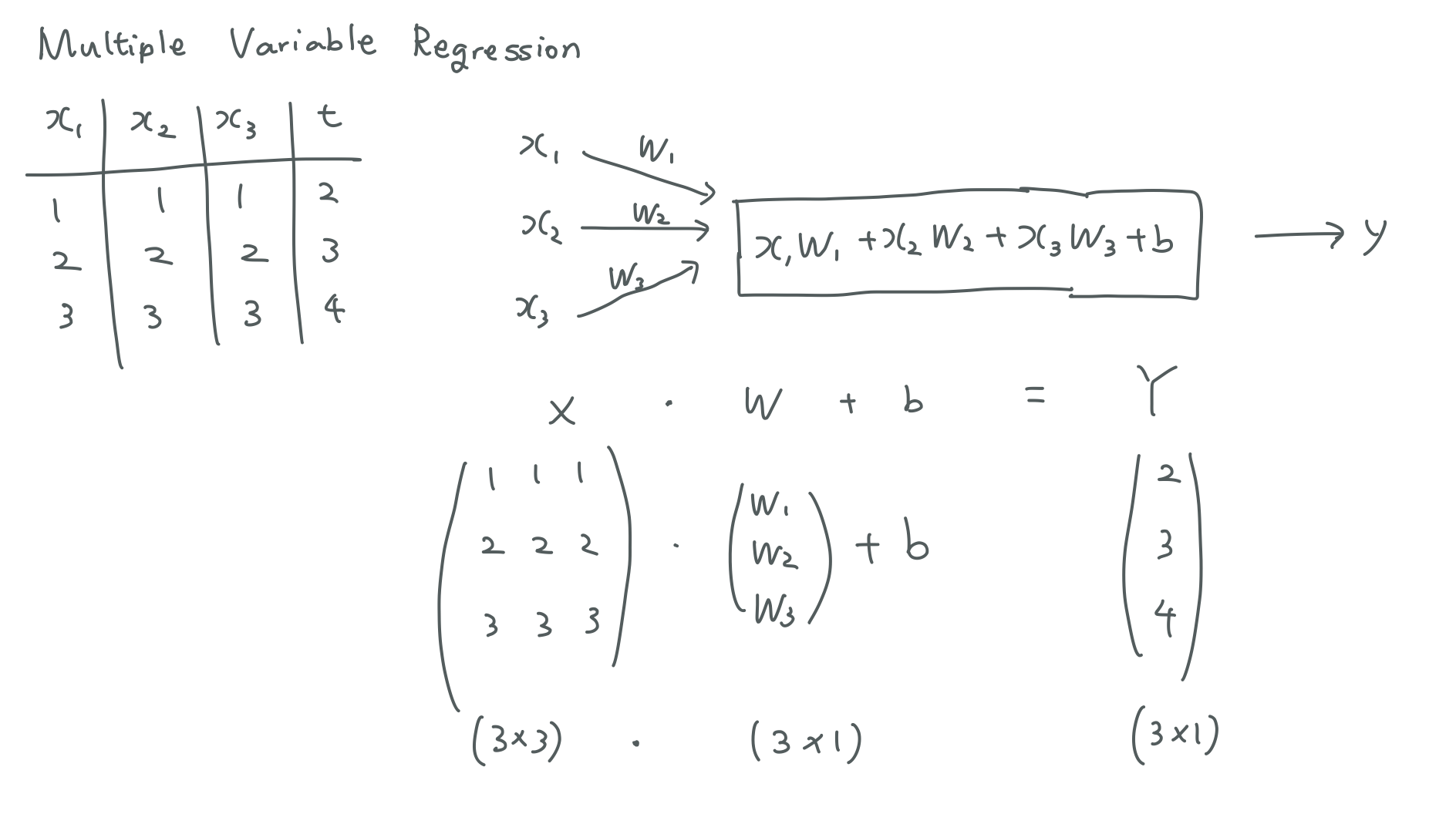
이 파일을 Training data 로 삼아 학습을 하도록 하겠습니다.
Training data 준비
load_data = np.loadtxt('./data.csv', delimiter=',', dtype=np.float32) # 입력 데이터와 출력 데이터 셋을 (5 * 1) 행렬로 변환(reshape) x_data = load_data[:, 0:-1] y_data = load_data[:, [-1]]임의의 W, b 준비
# 최초로 등록될 임의의 W, b 설정 # 0 ~ 1사이의 값으로 (3 * 1)짜리 matrix 생성 W = np.random.rand(3, 1) # 0 ~ 1 사이의 numpy scalar b = np.random.rand(1)학습
# 학습 가중치 learning_rate = 1e-5 f = lambda x: loss_func(x_data, y_data) print("Initial error value = ", error_val(x_data, y_data), "initial W = ", W, "initial b = ", b) for step in range(8001): # 학습 W -= learning_rate * numerical_derivative(f, W) b -= learning_rate * numerical_derivative(f, b) if step % 400 == 0: print("step = ", step, "error value = ", error_val(x_data, y_data), "W = ", W, "b = ", b) # 예측 print(predict([100,98,81]))결과

'인공지능' 카테고리의 다른 글
AI Logistic regression : 분류(Classification) (0) 2020.05.24 AI Linear regression 예제 (0) 2020.05.24 AI Gradient descent 알고리즘 (0) 2020.05.24 AI Linear Regression (0) 2020.05.24 AI 수치미분 Python 구현 (0) 2020.05.23