프로그래밍 언어 Semantic 표현

프로그래밍 언어 Semantic 표현은 어려워서 여러 가지 표현 방법들이 있어요

크게 Static(Formal) Semantics, Dynamic Semantics로 나뉘는데

 

Static Semantics

정적의미론은 BNF 만으로는 표현될 수 없는 규칙들을 표현하기 위해 고안된 것입니다.

대표적인 예시로 프로그램 내에서 어떤 변수는 참조되기 전에 선언된 상태여야 함이라는 규칙을 BNF로는 표현할 수 없습니다. (이건 증명됐다고하네요)

실제로 프로그래밍 언어에서는 이런 정적의미들을 컴파일 타임에 처리할 수 있는데 그래서 Static 이라는 이름이 붙여졌다고합니다.

 

- Attribute Grammars

 

Dynamic Semnatics

- Operational semantics

- Axiomatic semantics

- Denoatational semnatics

Attribute Grammars

프로그램 구문과 정적 의미론을 한 번에 표현할 수 있는 문법으로 Knuth 가 고안한 문법입니다.

Attribute Grammar = CFG + Semantic Rules(Attribute Equation)

 

간단한 예시

expr -> expr + term               { expr0.v = expr1.v + term.v }

     | term                                { expr.v = term.v }

term -> term * factor             { term0.v = term1,v * factor }

    | factor                               { term.v = factor.v }

factor -> number                   { factor.v = number.value }

    | ( expr )                             { factor.v = expr.v }

 

 

 

Attribute 종류

• synthesized attribute ( 아들 노드로부터 값이 결정 )
• inherited attribute ( 부모/조상 노드로부터 값이 결정 )
• intrinsic attribute ( 스스로 값을 지닌 노드 )

 

위 트리를 Attributed Tree 라고 합니다.

주의할 점은 Evaluate, 즉 수식의 평가(계산)는 DFS로 이루어진다는 것입니다. 따라서 노드의 아래쪽에서부터 값이 타고 올라온다~라고 생각하시면 좋습니다.

 

intrinsic attribute 는 대표적으로 변수들에 할당되는 속성입니다. 왜냐면 변수라는건 컴파일되면서 심볼테이블로 구축되어 어떤 변수가 어디에 있는지 심볼테이블에 저장되어 있고, 거기서부터 뽑아오는 정보이기 때문이죠 ( 부모나 자식 노드에서 오는게 아닙니다. )

 

술어 함수(Predicate Function)

술어 함수는 문법 규칙과 연관되며 모든 술어 함수는 논리형(boolean)으로 정의되어야 하고, 반드시 참이여야만 합니다.

거짓인 경우에는 구문 규칙이나 정적 의미론 규칙을 위배한 것으로 판단합니다.

단순 배정문에 대한 속성 문법 구문 규칙 : <assign> -> <var> = <expr> 의미론 규칙 : <expr>.expected_type  <- <var>.actual_type   구문 규칙 : <expr> -> <var>[2] + <var>[3] 의미론 규칙 : <expr>.actual_type  <-  if (<var>[2].actual_type = int ) and (<var>[3].actual_type = int) then int                                                           else real   end if 술어 함수 : <expr>.actual_type == <expr>.expected_type   구문 규칙 : <expr> -> <var> 의미론 규칙 : <expr>.actual_type  <-  <var>.actual_type 술어함수 : <expr>.actual_type == <expr>.expected_type   구문 규칙 : <var>  ->  A | B | C 의미론 규칙 : <var>.actual_type  <- look-up(<var>.string)   look-up 함수는 symbolc 테이블로부터 변수명을 찾아 그 타입을 리턴

+ 연산의 좌변과 우변의 타입이 다름을 허용하지 않는 문법 구문 규칙 : <assign> -> <var> = <expr> 의미론 규칙 : <expr>.expected_type  <-  <var>.actual_type   구문 규칙 : <expr> -> <var>[2] + <var>[3] 의미론 규칙 : <expr>.actual_type  <-  if (<var>[2].actual_type = int ) and ( <var>[3].actual_type = int ) then int                                                           else if (<var>[2].actual_type = real ) and ( <var>[3].actual_type = real ) then real                                                           else error   end if 술어 함수 : <expr>.actual_type == <expr>.expected_type   구문 규칙 : <expr> -> <var> 의미론 규칙 : <expr>.actual_type  <-  <var>.actual_type 술어 함수 : <expr>.actual_type == <expr>.expected_type   구문 규칙 : <var>  ->  A | B | C 의미론 규칙 : <var>.actual_type  <-  look-up(<var>.string)

 

Axiomatic Semantics ( 공리적 의미 )

Dynamic semantics 표기 방법 중 하나로 어떤 프로그램이 옳음을 수학적으로 증명하는 방법이에요

언어 자체를 표현한다기보다는 예시를 증명하는 방법을 써요

 

Assertion, precondition, postcondition 이라는 용어로 프로그램을 증명할 거예요

 

우리가 어떤 프로그램의 옳음을 실험적으로 증명하려면 모든 input을 다 넣어보고, 모든 output 이 옳게 나오는지 확인해봐야 해요

input의 정의역이 정수 전체라면 모든 정수의 조합을 넣어봐야 되겠지요. 이건 아무리 간단한 프로그램이더라도 몇십 년 이상 걸린다고 해요.

따라서 수학적 기법을 쓰는 건데 지금부터 그 규칙들을 소개할게요

 

Rule-1

{ P } S { Q }

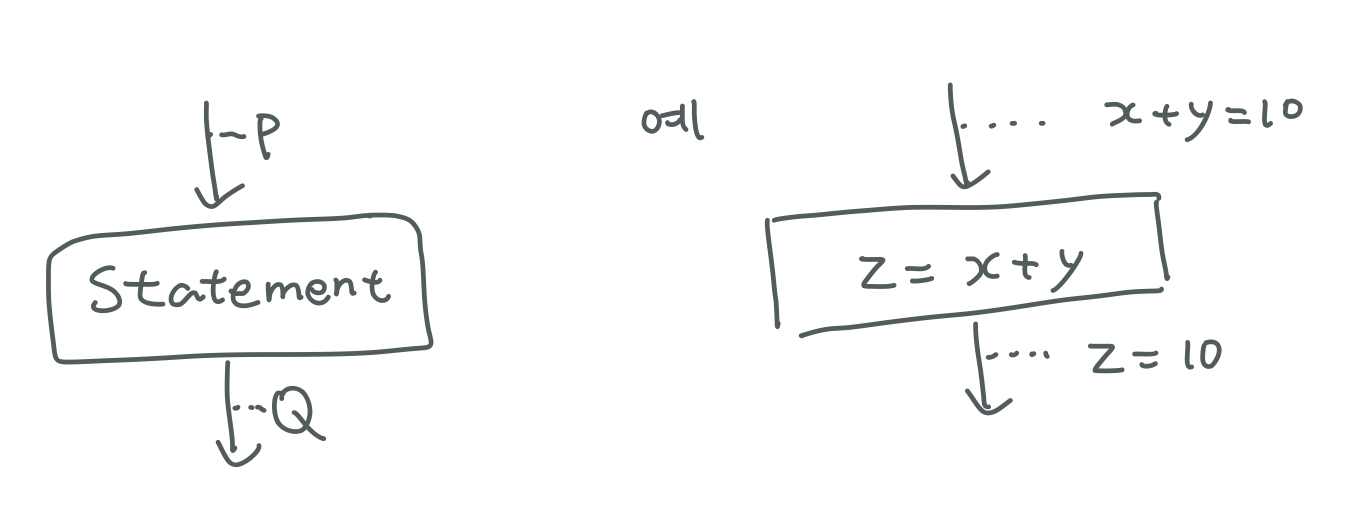
{ P } S { Q } 의 도식화

상태 P 가 Statement를 지나면 상태 Q가 된다는 것을 말해요. 이는 수학적인 과정을 거쳐야 하므로 자명한 내용이거나 별도의 증명이 수반되어야 합니다!

 

Rule-2

Q = P1 U P2 U P3 U ... U Pn

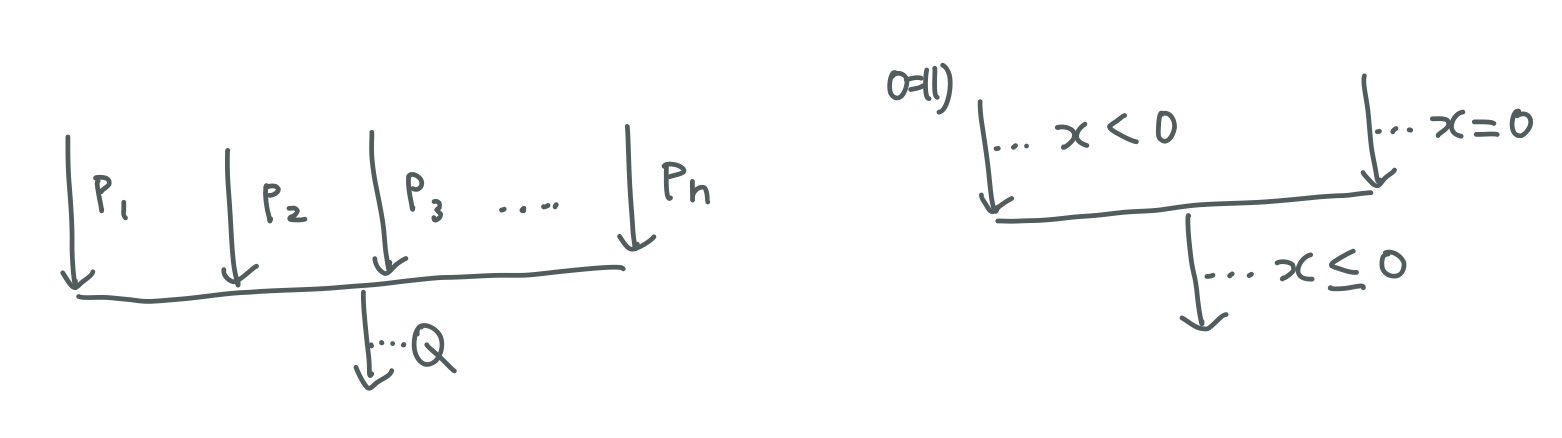
Q = P1 U P2 U P3 U ... U Pn 의 도식화

x < 0 과 x = 0 이 만나서 x <= 0 의 상태가 됨은 자명하죠?

이렇게 만나기 전의 x < 0, x = 0 을 강한 조건(strong condition), 합쳐진 이후의 x <= 0 을 약한 조건(weak condition)이라고 해요

 

Rule-3

Q1 : P and B    Q2 : P and ~B        ( ~ 는 not 을 의미합니다 )

Q1 : P and B, Q2 : P and ~B 의 도식화

x <= 0이라는 상태를 지니던 코드가 x == 0 을 기점으로 분기하게 되죠? true 쪽은 x = 0 의 상태를, false 쪽은 x < 0 이라는 상태를 갖게 돼요. 이를 수학적으로 쓰면 { x = 0 } : { x <= 0 } and { x == 0 }, { x < 0 } : { x <= 0 } and ~{ x == 0 } 가 됩니다~